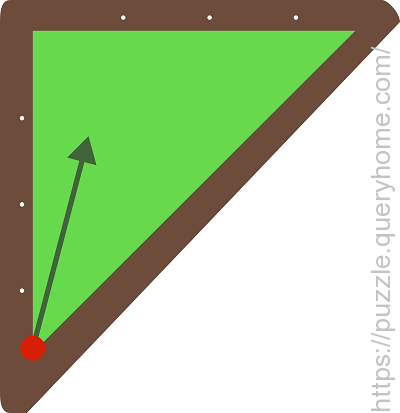
It is well known that, in a billiard table shaped like a right isosceles triangle as in the diagram below, a ball struck at the marked vertex cannot return to that same point after any number of reflections. The ball may bounce any number of times, and if the ball hits a vertex point as opposed to a side, then the reflections are absorbed.
Does this also hold true for non-right isosceles triangles?