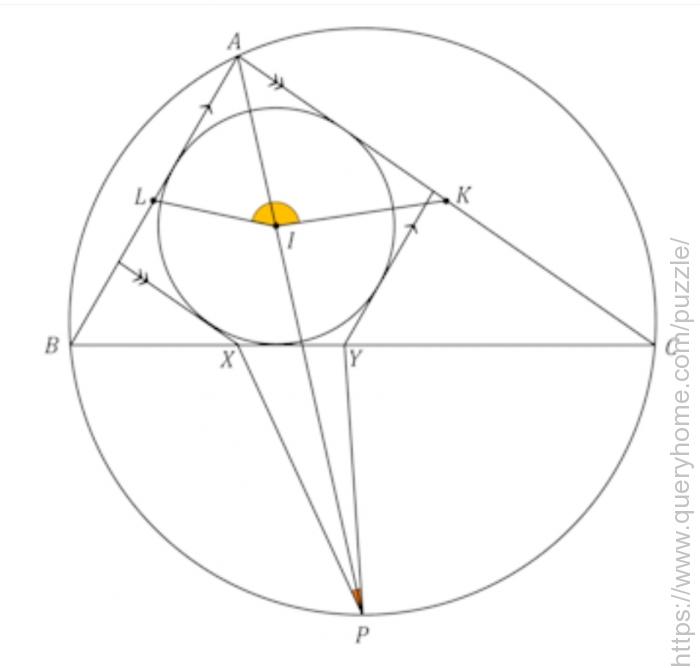
Let ABC be a triangle with AB < AC < BC. Let the incentre and incircle of triangle ABC be I and ω, respectively. Let X be the point on the line BC different from C such that the line through X parallel to AC is tangent to ω. Similarly, let Y be the point on the line BC different from B such that the line through Y parallel to AB is tangent to ω. Let AI intersect the circumcircle of triangle ABC again at P ≠ A. Let K and L be the midpoints of AC and AB, respectively.
Prove that ∠KIL + ∠YPX = 180°.