top button
Flag Notify
    Connect to us
      Site Registration

Site Registration

Find the shortest distance from the origin to the surface given by the equation xyz = k^3, where k is a given constant

0 votes
289 views
Find the shortest distance from the origin to the surface given by the equation xyz = k^3, where k is a given constant
posted May 6, 2015 by Ankit Kamboj

Looking for solution? Promote on:
Facebook Share Button Twitter Share Button LinkedIn Share Button




Similar Puzzles
0 votes
What is the shortest distance between circle A defined by (x − 5)2 + (y − 4)2 = 4 and circle B defined by (x − 1)2 .....

What is the shortest distance between circle A defined by (x − 5)2 + (y − 4)2 = 4 and circle B defined by (x − 1)2 + (y − 1)2 = 1? There is some point P on circle A closest to B, and there is another point Q on circle B closest to A. What are the coordinates of P and Q?
enter image description here

0 votes
If the centroid of a triangle is formed by the points (a,b), (b,c) and (c,a) is at the origin; then a^3 + b^3 + c^3 = ??

If the centroid of a triangle is formed by the points (a,b), (b,c) and (c,a) is at the origin i.e. (0,0) then a^3 + b^3 + c^3 = ??

+1 vote
Find the position in metres from the origin at which A overtakes B?

Two buses A and B are at positions 50 m and 100 m from the origin at time t = 0.
They start moving in the same direction simultaneously with uniform velocity of 10 m/s and 5 m/s.
Find the position in metres from the origin at which A overtakes B?

0 votes
A square pyramid has base PQRS and vertex O. Each edge has length equal to 20. Calculate the shortest distance..........

A square pyramid has base PQRS and vertex O.
Each edge has length equal to 20.
Calculate the shortest distance along the outer surface of the pyramid from P to T, the midpoint of OR.
enter image description here

+1 vote
What is the shortest distance that the spider must crawl in order to reach the fly?

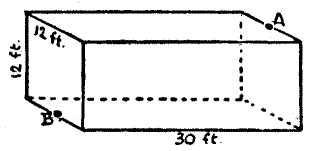
Spider and Fly

Inside a room as shown in the figure, measuring 30 feet in length and 12 feet in width and height, a spider is at a point on the middle of one of the end walls, 1 foot from the ceiling, as at A; and a fly is on the opposite wall, 1 foot from the floor in the centre, as shown in the figure at B. What is the shortest distance that the spider must crawl in order to reach the fly, which remains stationary? You can assume that that spider never drops or uses its web, but crawls fairly.

...