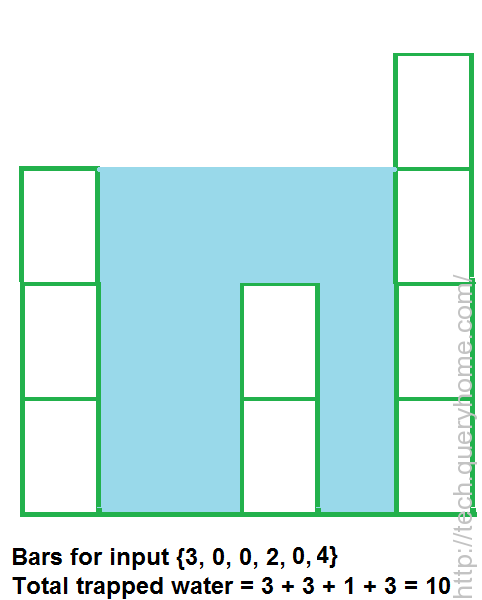
See the image, An element of array can store water if there are higher bars on left and right. We can find amount of water to be stored in every element by finding the heights of bars on left and right sides. The idea is to compute amount of water that can be stored in every element of array. For example, consider the array {3, 0, 0, 2, 0, 4}, we can store two units of water at indexes 1 and 2, and one unit of water at index 2.
A Simple Solution is to traverse every array element and find the highest bars on left and right sides. Take the smaller of two heights. The difference between smaller height and height of current element is the amount of water that can be stored in this array element. Time complexity of this solution is O(n2).
An Efficient Solution is to prre-compute highest bar on left and right of every bar in O(n) time. Then use these pre-computed values to find the amount of water in every array element. Below is C++ implementation of this solution.
// C++ program to find maximum amount of water that can
// be trapped within given set of bars.
#include<bits/stdc++.h>
using namespace std;
int findWater(int arr[], int n)
{
// left[i] contains height of tallest bar to the
// left of i'th bar including itself
int left[n];
// Right [i] contains height of tallest bar to
// the right of ith bar including itself
int right[n];
// Initialize result
int water = 0;
// Fill left array
left[0] = arr[0];
for (int i = 1; i < n; i++)
left[i] = max(left[i-1], arr[i]);
// Fill right array
right[n-1] = arr[n-1];
for (int i = n-2; i >= 0; i--)
right[i] = max(right[i+1], arr[i]);
// Calculate the accumulated water element by element
// consider the amount of water on i'th bar, the
// amount of water accumulated on this particular
// bar will be equal to min(left[i], right[i]) - arr[i] .
for (int i = 0; i < n; i++)
water += min(left[i],right[i]) - arr[i];
return water;
}
// Driver program
int main()
{
int arr[] = {0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1};
int n = sizeof(arr)/sizeof(arr[0]);
cout << "Maximum water that can be accumulated is "
<< findWater(arr, n);
return 0;
}
Output:
Maximum water that can be accumulated is 6
Time Complexity: O(n)
Auxiliary Space: O(n)
