Level order traversal of a tree is breadth first traversal for the tree.
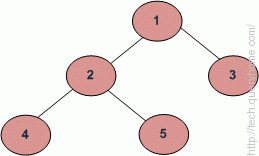
Level order traversal of the above tree is 1 2 3 4 5
METHOD 1 (Use function to print a given level)
Algorithm:
There are basically two functions in this method. One is to print all nodes at a given level (printGivenLevel), and other is to print level order traversal of the tree (printLevelorder). printLevelorder makes use of printGivenLevel to print nodes at all levels one by one starting from root.
/*Function to print level order traversal of tree*/
printLevelorder(tree)
for d = 1 to height(tree)
printGivenLevel(tree, d);
/*Function to print all nodes at a given level*/
printGivenLevel(tree, level)
if tree is NULL then return;
if level is 1, then
print(tree->data);
else if level greater than 1, then
printGivenLevel(tree->left, level-1);
printGivenLevel(tree->right, level-1);
Implementation:
// Recursive C program for level order traversal of Binary Tree
#include <stdio.h>
#include <stdlib.h>
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct node
{
int data;
struct node* left, *right;
};
/* Function protoypes */
void printGivenLevel(struct node* root, int level);
int height(struct node* node);
struct node* newNode(int data);
/* Function to print level order traversal a tree*/
void printLevelOrder(struct node* root)
{
int h = height(root);
int i;
for (i=1; i<=h; i++)
printGivenLevel(root, i);
}
/* Print nodes at a given level */
void printGivenLevel(struct node* root, int level)
{
if (root == NULL)
return;
if (level == 1)
printf("%d ", root->data);
else if (level > 1)
{
printGivenLevel(root->left, level-1);
printGivenLevel(root->right, level-1);
}
}
/* Compute the "height" of a tree -- the number of
nodes along the longest path from the root node
down to the farthest leaf node.*/
int height(struct node* node)
{
if (node==NULL)
return 0;
else
{
/* compute the height of each subtree */
int lheight = height(node->left);
int rheight = height(node->right);
/* use the larger one */
if (lheight > rheight)
return(lheight+1);
else return(rheight+1);
}
}
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newNode(int data)
{
struct node* node = (struct node*)
malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return(node);
}
/* Driver program to test above functions*/
int main()
{
struct node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
printf("Level Order traversal of binary tree is \n");
printLevelOrder(root);
return 0;
}
Output:
Level order traversal of binary tree is
1 2 3 4 5
Time Complexity: O(n^2) in worst case. For a skewed tree, printGivenLevel() takes O(n) time where n is the number of nodes in the skewed tree. So time complexity of printLevelOrder() is O(n) + O(n-1) + O(n-2) + .. + O(1) which is O(n^2).
