Question

How to traverse a binary search tree diagonally? Any sample algo/code?

Answer 1

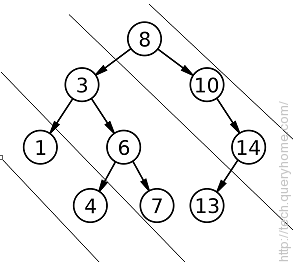
Inputs : shown in Image.
Output :
Diagonal Traversal of binary tree :
8 10 14
3 6 7 13
1 4

---Sample Code---

// C++ program for diagnoal traversal of Binary Tree
#include <bits/stdc++.h>
using namespace std;

// Tree node
struct Node
{
    int data;
    Node *left, *right;
};

/* root - root of the binary tree
   d -  distance of current line from rightmost
        -topmost slope.
   diagonalPrint - multimap to store Diagonal
                   elements (Passed by Reference) */
void diagonalPrintUtil(Node* root, int d,
                      map<int, vector<int>> &diagonalPrint)
{
    // Base case
    if (!root)
        return;

    // Store all nodes of same line together as a vector
    diagonalPrint[d].push_back(root->data);

    // Increase the vertical distance if left child
    diagonalPrintUtil(root->left, d + 1, diagonalPrint);

    // Vertical distance remains same for right child
    diagonalPrintUtil(root->right, d, diagonalPrint);
}

// Print diagonal traversal of given binary tree
void diagonalPrint(Node* root)
{
    // create a map of vectors to store Diagonal elements
    map<int, vector<int> > diagonalPrint;
    diagonalPrintUtil(root, 0, diagonalPrint);

    cout << "Diagonal Traversal of binary tree : \n";
    for (auto it = diagonalPrint.begin();
         it != diagonalPrint.end(); ++it)
    {
        for (auto itr = it->second.begin();
             itr != it->second.end(); ++itr)
            cout << *itr  << ' ';

        cout << '\n';
    }
}

// Utility method to create a new node
Node* newNode(int data)
{
    Node* node = new Node;
    node->data = data;
    node->left = node->right = NULL;
    return node;
}

// Driver program
int main()
{
    Node* root = newNode(8);
    root->left = newNode(3);
    root->right = newNode(10);
    root->left->left = newNode(1);
    root->left->right = newNode(6);
    root->right->right = newNode(14);
    root->right->right->left = newNode(13);
    root->left->right->left = newNode(4);
    root->left->right->right = newNode(7);

    diagonalPrint(root);

    return 0;
}