Mergesort - A Summary

Merge sort is based on the divide-and-conquer paradigm. Its worst-case running time has a lower order of growth than insertion sort. Like heap sort, merge sort requires additional memory proportional to the size of the input for scratch space, but, unlike heap sort, merge sort is stable, meaning that "equal" elements are ordered the same once sorting is complete.

To sort A[p .. r]:
1. Divide Step If a given array A has zero or one element, simply return; it is already sorted. Otherwise, split A[p .. r] into two subarrays A[p .. q] and A[q + 1 .. r], each containing about half of the elements of A[p .. r]. That is, q is the halfway point of A[p .. r].
2. Conquer Step Conquer by recursively sorting the two subarrays A[p .. q] and A[q + 1 .. r].
3. Combine Step Combine the elements back in A[p .. r] by merging the two sorted subarrays A[p .. q] and A[q + 1 .. r] into a sorted sequence. To accomplish this step, we will define a procedure MERGE (A, p, q, r).

Algorithm

MERGE-SORT (A, p, r)
{
    IF p < r                                                   
         THEN q = FLOOR[(p + r)/2]                 
                 MERGE (A, p, q)                        
                 MERGE (A, q + 1, r)                    
                 MERGE (A, p, q, r)                      
}

MERGE (A, p, q, r )
{
.     n1 ← q − p + 1
      n2 ← r − q
      Create arrays L[1 . . n1 + 1] and R[1 . . n2 + 1]
      FOR i ← 1 TO n1
            DO L[i] ← A[p + i − 1]
      FOR j ← 1 TO n2
            DO R[j] ← A[q + j ]
      L[n1 + 1] ← ∞
      R[n2 + 1] ← ∞
      i ← 1
      j ← 1
     FOR k ← p TO r
         DO IF L[i ] ≤ R[ j]
                THEN A[k] ← L[i]
                        i ← i + 1
               ELSE A[k] ← R[j]
                        j ← j + 1
}

Graphical Representation

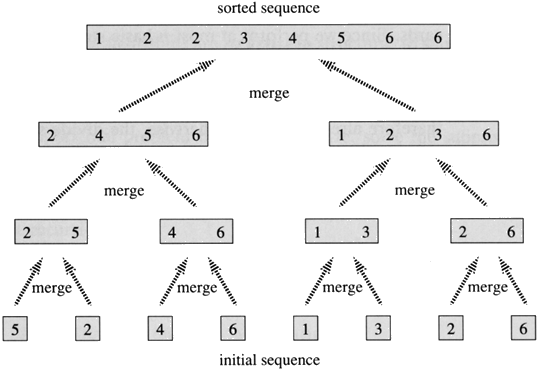
C Implementation

void mergeSort(int numbers[], int temp[], int array_size) 
{
    m_sort(numbers, temp, 0, array_size - 1);    
} 

void m_sort(int numbers[], int temp[], int left, int right)
{
    int mid;
    if (right > left)
    {
        mid = (right + left) / 2;
        m_sort(numbers, temp, left, mid);
        m_sort(numbers, temp, mid+1, right);
        merge(numbers, temp, left, mid+1, right);
    }
}

void merge(int numbers[], int temp[], int left, int mid, int right)
{
    int i, left_end, num_elements, tmp_pos;
    left_end = mid - 1;
    tmp_pos = left;
    num_elements = right - left + 1;
    while ((left <= left_end) && (mid <= right))
    {
        if (numbers[left] <= numbers[mid])
        {
            temp[tmp_pos] = numbers[left];
            tmp_pos = tmp_pos + 1;
            left = left +1;
        }
        else
        {
            temp[tmp_pos] = numbers[mid];
            tmp_pos = tmp_pos + 1;
            mid = mid + 1;
        }
    }

    while (left <= left_end)
    {
        temp[tmp_pos] = numbers[left];
        left = left + 1;
        tmp_pos = tmp_pos + 1;
    }

    while (mid <= right)
    {
        temp[tmp_pos] = numbers[mid];
        mid = mid + 1;
        tmp_pos = tmp_pos + 1;
    }

    for (i = 0; i <= num_elements; i++)
    {
        numbers[right] = temp[right];
        right = right - 1;
    }
}

Summary Merge sort is a fast, stable sorting routine with guaranteed O(n*log(n)) efficiency. When sorting arrays, merge sort requires additional scratch space proportional to the size of the input array. Merge sort is relatively simple to code and offers performance typically only slightly below that of quicksort.

QuickSort Algorithm (A Summary)

Quicksort is a sorting algorithm that uses the divide and conquer strategy. This algorithm finds the element called pivot , that partitions the array into two halves in such a way that the elements in the left sub array are less then and the elements in the right subarrays are are greater then the pivot element. And we apply the same algorithm on left subarray and right subarray separately (recursive).

Steps of Quicksort

1) Divide :Rearrange the elements and split the array into two sub arrays and an element in between .Each element in the left sub array is less than or equal to the middle element and each element in the right sub array is greater than the middle element.
2) Conquer : Apply step 1 recursively on two sub arrays.
3) Combine : Combine all the sorted elements in a group to form a list if sorted elements.

Example: We will sort an array
A = (38 81 22 48 13 69 93 14 45 58 79 72)
with quicksort, always choosing the pivot element to be the element in position (left + right)/2.
During the partitioning process,
i) Elements strictly to the left of position lo are less than or equivalent to the pivot element (69).
ii) Elements strictly to the right of position hi are greater than the pivot element. When lo and hi cross, we are done. The final value of hi is the position in which the partitioning element ends up.

Algorithm

partition( A, left, right) rarranges A[left..right] and finds and returns an integer q, such that
A[left], ..., A[q–1] <∼ pivot, A[q] = pivot, A[q+1], ..., A[right] > pivot,

Integer partition( T A[], Integer left, Integer right) 
 m = (left +right) / 2; 
 swap( A[left], A[m]); 
 pivot = A[left]; 
 lo = left+1; 
 hi = right; 
 while(lo ≤ hi) 
   while(A[hi] > pivot )  
     hi = hi – 1; 
   while(lo ≤ hi and A[lo] <∼ pivot ) 
     lo = lo + 1; 
   if (lo ≤ hi)  
     swap( A[lo], A[hi]); 
     lo = lo + 1; 
     hi = hi – 1; 
 swap(A[left], A[hi]); 
 return hi

quicksort( A, left, right) sorts A[left..right] by using partition() to partition A[left..right], and then calling itself recursively twice to sort the two subarrays.

void quicksort( T A[], Integer left, Integer right) 
 if (left < right ) 
  q = partition( A, left, right); 
  quicksort( A, left, q–1); 
  quicksort( A, q+1, right);

Complexity

Worst-case O(N2) This happens when the pivot is the smallest (or the largest) element. Then one of the partitions is empty, and we repeat recursively the procedure for N-1 elements.
Best-case O(NlogN) The best case is when the pivot is the median of the array, and then the left and the right part will have same size.
Average-case O(NlogN)

Mergesort - A Summary

Algorithm

Graphical Representation

C Implementation

References

Your comment on this post:

Related Articles

Steps of Quicksort

Algorithm

Complexity