What is a Cousin of a Node
Cousin of a node is a node or nodes which are at the same level but dont share the same parent. See the following image in which 12, 23, 54 and 76 are at the same level in which we can say 54 and 76 are the cousins of the node 12. Similarly 19 and 67 are the cousins of 9 and 14.
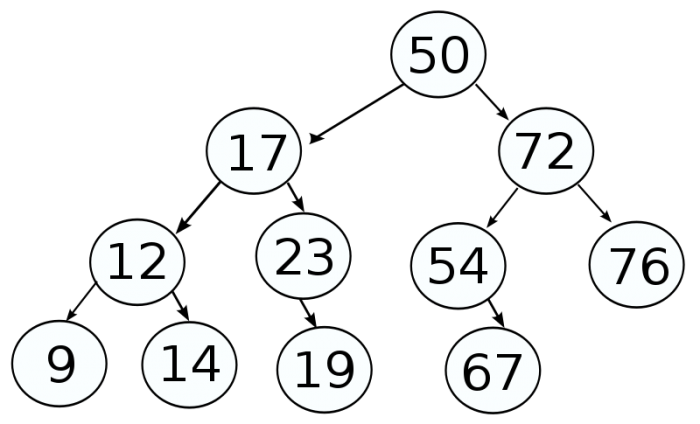
How to find the cousins of the Node
Logic is very simple you need to find out the level of given node and its parent. Once you know the parent the job is easy i.e. traverse each node and check its level if level is same as given node level and its parent is not same as given node then its cousin or not.
Code in C++
(picked from one of my old post)
using namespace std;
struct node{
struct node* left;
struct node* right;
int data;
};
using namespace std;
struct node{
struct node* left;
struct node* right;
int data;
};
// Traverse the tree in a way so that you can preserve the level and compare it with given level
void inorder(struct node* root,int present_level,int level,struct node* parent)
{
if(root!=NULL)
{
if(parent!=root)
inorder(root->left,present_level+1,level,parent);
if(level==present_level)
cout<<root->data<<" ";
if(parent!=root)
inorder(root->right,present_level+1,level,parent);
}
}
void make_tree(struct node **root,int data)
{
if((*root)==NULL)
{
(*root)=new node;
(*root)->left=NULL;
(*root)->right=NULL;
(*root)->data=data;
return;
}
else
{
if (((*root)->data)< data)
make_tree(&((*root)->right),data);
else
make_tree(&((*root)->left),data);
}
}
int height(struct node* node)
{
if (node==NULL)
return 0;
else
{
int lDepth = height(node->left);
int rDepth = height(node->right);
/* use the larger one */
if (lDepth > rDepth)
return(lDepth+1);
else return(rDepth+1);
}
}
void print_level(node *root, int space, int level, int currlevel)
{
int i =0;
if ( currlevel == level )
{
for (i = 0; i < space; i++)
printf(" ");
if (root == NULL)
printf(" ");
else
printf("%d",root->data);
for (i = 0; i < space; i++)
printf(" ");
}
else
{
if(!root)
{
print_level(NULL, space, level, currlevel + 1);
print_level(NULL, space, level, currlevel + 1);
}
else
{
print_level(root->left, space, level, currlevel + 1);
print_level(root->right, space, level, currlevel + 1);
}
}
}
void print_tree(node *tree)
{
int hght = height(tree);
int width = (1 << ( hght + 1)) - 1;
int space = width / 2; int i;
for (i = 1; i <= hght; i++)
{
print_level(tree, space, i, 1);
printf("\n\n");
space = space / 2;
}
}
struct node* find_level_and_parent(struct node* root,int data,int* level)
{
struct node* parent=NULL;
struct node* child=root;
while(1)
{
if(child==NULL)
return NULL;
if(child->data==data)
{
return parent;
}
if(data>child->data)
{
parent=child;
child=child->right;
*level=*level+1;
}
else if(data<=child->data)
{
parent=child;
child=child->left;
*level=*level+1;
}
}
}
int main()
{
struct node* root=NULL;
make_tree(&root,50);
make_tree(&root,17);
make_tree(&root,72);
make_tree(&root,12);
make_tree(&root,23);
make_tree(&root,34);
make_tree(&root,54);
make_tree(&root,76);
make_tree(&root,9);
make_tree(&root,14);
make_tree(&root,19);
make_tree(&root,67);
print_tree(root);
int level=0;
struct node* temp=find_level_and_parent(root,12,&level);
if(temp!=NULL)
{
inorder(root,0,level,temp);
return 0;
}
return 1;
}
