top button
Flag Notify
    Connect to us
      Site Registration

Site Registration

Three non-concentric circles of equal radii are drawn such that each circle touches the other two externally...

0 votes
744 views

Three non-concentric circles of equal radii are drawn such that each circle touches the other two externally. The centres are joined to form a triangle whose area is 17320.5 cm^2. Find the area of the triangle not included in the circles.

Area not included in triangles

posted Oct 30, 2015 by anonymous

Share this puzzle
Facebook Share Button Twitter Share Button LinkedIn Share Button

1 Answer (Check Answer ▼)





Similar Puzzles
+1 vote
Two congruent circles of radius 5 cm are drawn in such a way that one is 1 cm below other. Area of red coloured region?

Two congruent circles of radius 5 cm are drawn in such a way that one is 1 cm below the other . Find the area of red coloured region?

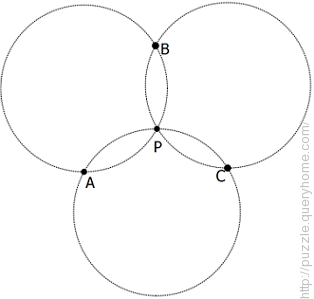
enter image description here

0 votes
I have 3 unit circles. Two of them are externally tangent to each other. The third one passes through tangent point...

I have 3 unit circles. Two of them are externally tangent to each other. The third one passes through the tangent point, cutting two symmetrical areas from those two circles, as shown in the diagram. What is the shaded area?

enter image description here

0 votes
Three congruent circles are pairwise tangent and each has a radius equal to 2. A circle circumscribes..............

Three congruent circles are pairwise tangent and each has a radius equal to 2. A circle circumscribes the three circles. Calculate the total area shaded in blue. The blue region is comprised of two parts. One region is the three circular sectors of the small circles enclosed by the line segments connecting the three small circle’s centers. The other region is outside the three small circles and bound by the large circumscribing circle (exclude the area in between the three small circles).
enter image description here

+3 votes
Three circles of equal radii all intersect at a single point as shown in figure, which of the following must be true?

Three circles of equal radii all intersect at a single point P. Let the other intersections be A, B and C. Which of the following must be true?

a) P is the incentre of Triangle ABC
b) P is the circumcentre of Triangle ABC
c) P is the centroid of Triangle ABC
d) P is the orthocenter of Triangle ABC

enter image description here

0 votes
In a square with a side length of 1, two quarter circles are drawn...........What is the radius of the inscribed circle?

In a square with a side length of 1, two quarter circles are drawn and a circle is inscribed between the quarter circles, as shown in the diagram.
What is the radius of the inscribed circle?

enter image description here

...