top button
Flag Notify
    Connect to us
      Site Registration

Site Registration

A triangle has a bug on each corner. If each walks in random direction, find probability of no bug crashs with other?

0 votes
338 views

There is an equilateral triangle and three bugs are sitting on the three corners of the triangle. Each of the bugs picks up a random direction and starts walking along the edge of the equilateral triangle. What is the probability that none of the bugs crash into each other?

posted Mar 31, 2017 by Deepa

Share this puzzle
Facebook Share Button Twitter Share Button LinkedIn Share Button

1 Answer

+1 vote

Out of the eight possible outcomes ( 2×2×2 ) only 2 possibilities ( All the ants moving clockwise or anticlockwise ) allow the ants to not cross path with each other. Therefore the probability that the ants won't crash each other on this scenario is = 2/8 = 1/4 = 25%.

answer Mar 31, 2017 by Tejas Naik



Similar Puzzles
0 votes
Triangle ABC with random points on the circle. What is the probability of triangle covering the centre of the circle?

Triangle ABC is stuck in a circle. Its points are on random areas on the circumference of the circle. What is the probability of the triangle covering the centre of the circle?
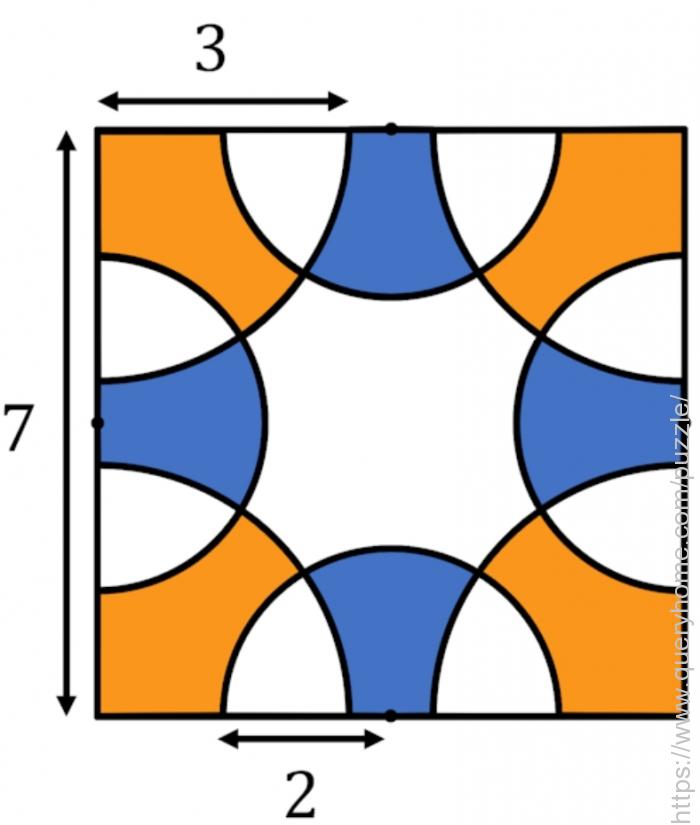
enter image description here

0 votes
A square has a side length of 7. On each corner, a quarter circle with radius 3 is constructed with the corner........

A square has a side length of 7. On each corner, a quarter circle with radius 3 is constructed with the corner as its center. And on the midpoint of each side, a semicircle with radius 2 is constructed with the midpoint as its center. What is the difference between the orange shaded areas and the blue shaded areas?
enter image description here

0 votes
Three spheres are tangent to a plane at the vertices of a triangle and are tangent to each other. Find the radii........

Three spheres are tangent to a plane at the vertices of a triangle and are tangent to each other. Find the radii of the spheres if the sides of the triangle are 6, 8, and 10.
enter image description here

0 votes
A right triangle has a semicircles with radii of 3 and 4 on its legs, as shown. The semicircles intersect along.........

A right triangle has a semicircles with radii of 3 and 4 on its legs, as shown. The semicircles intersect along the hypotenuse. What is the shaded area?
enter image description here

0 votes
A boy started from one corner of a rectangular path and walks along the adjacent sides to reach opposite corner.........

A boy started from one corner of a rectangular path and walks along the adjacent sides to reach opposite corner.
If he had walked through a shortest distance diagonally, he could have saved the distance equal to five-sixth of the shortest side a park, then what is the ratio of a longest side to the shortest side?

...