The answer is ===> C] As far as he wants.
If you start up with n books than the book on the table must start with (1/2n)th of its length in overhang { Overhang is the distance from the tip of the book to the edge of the table or the underlying book }. The subsequent books can then have (1/2(n-1))th overhang {which is greater than the previous overhang} and so on until the final book that can overhang half of its length.
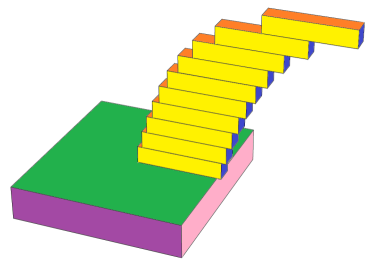
In other words the overhang can increase as we go above in the stack and if there are infinite books theoretically it can have an overhang of:
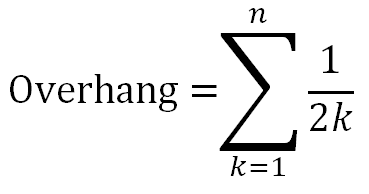
This is a divergent sum ie., if there are infinite terms the sum also reaches infinity. Therefore the answer is C.
