When you have to store a set of strings, what data structure should you use? You could use hash tables, which sprinkle the strings throughout an array. Access is fast, but information about relative order is lost. Another option is the use of binary search trees, which store strings in order, and are fairly fast. Or you could use digital search tries, which are lightning fast, but use lots of space.
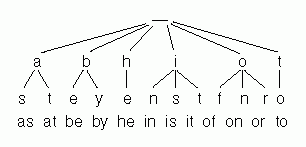
A binary search tree for 12 words.
Digital search tries store strings character by character. given Figure is a tree that represents the same set of 12 words; each input word is shown beneath the node that represents it. (Two-letter words lead to prettier pictures; all structures that we'll see can store variable-length words.) In a tree representing words of lowercase letters, each node has 26-way branching (though most branches are empty, and not shown in Figure ). Searches are very fast: A search for "is" starts at the root, takes the "i" branch, then the "s" branch, and ends at the desired node. At every node, we access an array element (one of 26), test for null, and take a branch. Unfortunately, search tries have exorbitant space requirements: Nodes with 26-way branching typically occupy 104 bytes, and 256-way nodes consume a kilobyte. Eight nodes representing the 34,000-character Unicode Standard would together require more than a megabyte!