Summary on bubble sort

Bubble Sort:-

Bubble sort is a simple sorting algorithm. This sorting algorithm is comparison-based algorithm in which each pair of adjacent elements is compared and the elements are swapped if they are not in order. Bubble sort algorithm starts by comparing the first two elements of an array and swapping if necessary, i.e., if you want to sort the elements of array in ascending order and if the first element is greater than second then, you need to swap the elements but, if the first element is smaller than second, you mustn't swap the element. Then, again second and third elements are compared and swapped if it is necessary and this process go on until last and second last element is compared and swapped.

Note: If there are n elements to be sorted then, the process mentioned above should be repeated n-1 times to get required result.

Algorithm:-

Step 1: Repeat Steps 2 and 3 for i=1 to 10

Step 2: Set j=1

Step 3: Repeat while j<=n

         (A) if  a[i] < a[j]

             Then interchange a[i] and a[j]

             [End of if]

         (B) Set j = j+1
        [End of Inner Loop]

    [End of Step 1 Outer Loop]

Step 4: Exit

Pictorial Representation

C program for bubble sort

#include<stdio.h> //header files

#include<conio.h>

void bubble_sort(int[], int);

void main() //starting of main function

{

   int arr[30], num, i; //array of size 30

  printf("\nEnter no of elements :");

   scanf("%d", &num);

   printf("\nEnter array elements :");

   for (i = 0; i < num; i++)

   scanf("%d", &arr[i]);

   bubble_sort(arr, num); //calling the function

   getch(); //to hold the screen

}

void bubble_sort(int iarr[], int num)

{

   int i, j, k, temp;

   printf("\nUnsorted Data:");

   for (k = 0; k < num; k++)

  {

      printf("%5d", iarr[k]);

}

for (i = 1; i < num; i++)

{

      for (j = 0; j < num - 1; j++)

{

if (iarr[j] > iarr[j + 1])

{

            temp = iarr[j];

            iarr[j] = iarr[j + 1];

            iarr[j + 1] = temp;

}

}

printf("\nAfter pass %d : ", i);

      for (k = 0; k < num; k++)

{

         printf("%5d", iarr[k]);

}

}

}

Complexity:-

Algorithm	Worst case	Average case	Best case
Bubble sort	O(n²)	O(n²)	O(n)

Summary on insertion sort

Insertion Sort:

Insertion Sort is implemented by inserting a particular element at the appropriate position. The number of iterations used by this sorting technique depends on the number of items in the array. In general, if there are n items in the array, then (n-1) iterations are used. Here, we are going to implement this algorithm using C. In C, the array index starts from 0.

Algorithm:

1) Start.
2) Assume that there are n elements in the list of items to be sorted.
3) Set i=1,j=0.
4) Compare the element at the i^th position and the element at the j^th position.
a) If a[i] is greater than a[j] do the steps (i),(ii),(iii)
i) temp=a[j]
ii) a[j]=a[i]
iii) Check if shifting is required. If so, do steps Ò
Ò k=i
Ò f (k is greater than j do step ►
► a[k]=a[k-1]
► k=k-1
► go to Step (a)
Ò a[k+1]=temp
b) j=j+1
if(j<1) go to Step (a)
Otherwise
i=i+1
j=0
if(i<=n-1) go to Step (a)
5) Print the elements in the array a
6) Stop.

During the first iteration, the element at the 1^st position is compared with the element at the 0^th position. During the second iteration, the element at the 2^nd position is compared with elements at the 0^th and 1^st positions. This process is repeated for all the elements in the array up to (n-1)^st iteration. This method is widely used by card players.

Pictorial Representation

Corresponding C program

#include<stdio.h> //Header Files
#include<conio.h>
#include<math.h>
#include<stdlib.h>
void main()
{
void isort(int a[],int);
int s,a[50],t,n,i,j,k;
clrscr();
printf("Enter Total nos:");
scanf("%d",&n);
printf("\nEnter the Items 1 by 1:");
for(i=0;i<n;i++)
scanf("%d",&a[i]);
isort(a,n);
getch();
}
void isort(int x[],int n)
{
int k,y,i;
for(k=1;k<n;k++)
{
y=x[k];
for(i=k-1;i>=0;i--)
{
if(y>=x[i])
break;
x[i+1]=x[i];
}
x[i+1]=y;
}

printf("The Sorted Numbers are:\n");
for(k=0;k<n;k++)
printf("%d ",x[k]);
}

Complexity The complexity of the insertion sort algorithm is shown in the following table.

Algorithm	Worst case	Average case	Best case
Insertion sort	O(n²)	O(n²)	O(n-1)

Short notes on Quick Sort

Quick Sort

Quick sort is a very popular sorting method. This sort name comes from the fact that quick sort can sort a list of data elements significantly faster than any of the common sorting algorithms. This sorting uses a strategy called divide and conquer. It is based on the principle that is faster and easier to sort two small arrays than one larger one.

The sequence of steps required to perform a quick sort operation on a set of elements of the array are as follows.

A pivot item near the middle of the array is chosen. Let it be x.
Now scan the array from left to right until some element e.g., a_i>x is encountered.
Now scan the array from right to left until some element e.g.,a_j<x is encountered.
Now exchange the items ai and aj.
Again repeat steps 2 to 4 until the scan operation meets somewhere in the middle of the array.

Quick sort is also called partition exchange sort and it was invented by C.A.R. Hoare. The average execution time of quick sort is O(n(log₂n)²) and this sort is good for large sorting jobs.

Pictorial Representation

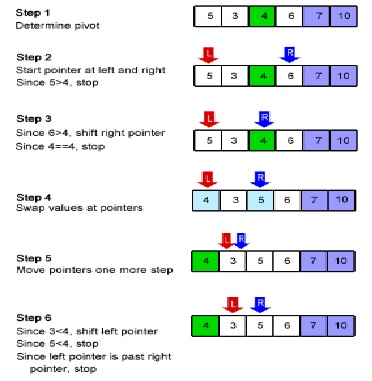
Quick Sort Algorithm

1. If n < = 1, then return.

2. Pick any element V in a[]. This is called the pivot.

3. Rearrange elements of the array by moving all elements xi > V right of V and all elements xi < = V left of V. If the place of the V after re-arrangement is j, all elements with value less than V, appear in a[0], a[1] . . . . a[j – 1] and all those with value greater than V appear in a[j + 1] . . . . a[n – 1].

4. Apply quick sort recursively to a[0] . . . . a[j – 1] and to a[j + 1] . . . . a[n – 1].

Program for Quick Sort

#include <stdio.h>
void quick_sort(int[], int, int);
int partition(int[], int, int);
int main()
{
   int a[50], n, i;
   printf("How many elements?");
   scanf("%d", & n);
   printf("\nEnter array elements:");
   for (i = 0; i < n; i++)
   {
       scanf("%d", & a[i]);
   }
   quick_sort(a, 0, n - 1);
   printf("\nArray after sorting:");
   for (i = 0; i < n; i++)
   {
       printf("%d ", a[i]);
   }

   return 0;
}

void quick_sort(int a[], int l, int u)
{
   int j;
   if (l < u)
   {
       j = partition(a, l, u);
       quick_sort(a, l, j - 1);
       quick_sort(a, j + 1, u);
   }
}

int partition(int a[], int l, int u)
{
   int v, i, j, temp;
   v = a[l];
   i = l;
   j = u + 1;
   do
   {
       do
{
           i++;
}
       while (a[i] < v && i <= u);
       do
{
           j--;
}
       while (v < a[j]);
       if (i < j)
       {
           temp = a[i];
           a[i] = a[j];
           a[j] = temp;
       }
   }
   while (i < j);
   a[l] = a[j];
   a[j] = v;
   return (j);
}

The complexity of the quick sort algorithm is given in the following table.

Algorithm	Worst case	Average case	Best case
Quick sort	O(n)²	log₂n	log₂n

The Selection Sort

Selection Sort:-

Selection sort is a simple sorting algorithm. This sorting algorithm is an in-place comparison-based algorithm in which the list is divided into two parts, the sorted part at the left end and the unsorted part at the right end. Initially, the sorted part is empty and the unsorted part is the entire list.The smallest element is selected from the unsorted array and swapped with the leftmost element, and that element becomes a part of the sorted array. This process continues moving unsorted array boundary by one element to the right.

This process continues and requires n−1 passes to sort n items, since the final item must be in place after the (n−1) st pass.

This algorithm is not suitable for large data sets as its average and worst case complexities are of Ο(n²), where n is the number of items.

Algorithm:-

Step 1 − Set MIN to location 0
Step 2 − Search the minimum element in the list
Step 3 − Swap with value at location MIN
Step 4 − Increment MIN to point to next element
Step 5 − Repeat until list is sorted.

Pictorial Representation:-

In the first pass, the smallest element found is 1, so it is placed at the first position, then leaving first element, smallest element is searched from the rest of the elements, 3 is the smallest, so it is then placed at the second position. Then we leave 1 and 3, from the rest of the elements, we search for the smallest and put it at third position and keep doing this, until array is sorted.

C program for selection sort:-

#include <stdio.h>
#include <stdbool.h>
#define MAX 7

int intArray[MAX] = {4,6,3,2,1,9,7};

void printline(int count) {
   int i;
	
   for(i = 0;i <count-1;i++) {
      printf("=");
   }
	
   printf("=\n");
}

void display() {
   int i;
   printf("[");
	
   // navigate through all items 
   for(i = 0;i<MAX;i++) {
      printf("%d ", intArray[i]);
   }
	
   printf("]\n");
}

void selectionSort() {

   int indexMin,i,j;
	
   // loop through all numbers 
   for(i = 0; i < MAX-1; i++) { 
	
      // set current element as minimum 
      indexMin = i;
		
      // check the element to be minimum 
      for(j = i+1;j<MAX;j++) {
         if(intArray[j] < intArray[indexMin]) {
            indexMin = j;
         }
      }

      if(indexMin != i) {
         printf("Items swapped: [ %d, %d ]\n" , intArray[i], intArray[indexMin]); 
			
         // swap the numbers 
         int temp = intArray[indexMin];
         intArray[indexMin] = intArray[i];
         intArray[i] = temp;
      }          

      printf("Iteration %d#:",(i+1));
      display();
   }
}  

main() {
   printf("Input Array: ");
   display();
   printline(50);
   selectionSort();
   printf("Output Array: ");
   display();
   printline(50);
}

Complexity:-

Algorithm	Worst case	Average case	Best case
Bubble sort	O(n²)	O(n²)	O(n²)

Its worst case would be when the array is in reversed order. In that case, it would perform O(n²).

For average case too its performance is O(n²).

https://www.youtube.com/watch?v=xWBP4lzkoyM

Summary on bubble sort

Your comment on this post:

Related Articles