By using the Rational Roots Test we can check for +/-(1,2,3,6/1) as possible roots and when we check for x= -3 & -2 we get
LHS = RHS.
So the 3 roots are x = 1, -2 & -3.
Alternatively, we can use the info that (x-1) is divisible. Here Synthetic divisions using coefficients can be very handy as shown below:
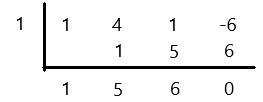
which means the quotient after division = (x^2 + 5x + 6)
In other words (x^3 + 4x^2 + x - 6) = 0 = (x - 1)(x^2 + 5x + 6)
Now its easy to get the roots of the quadratic equation
x^2 + 5x + 6 = 0
x^2 + 3x + 2x + 6 = 0
x(x + 3) + 2(x + 3) = 0
x = -3, -2.
